First-Order Manifold Data Augmentation for Regression Learning
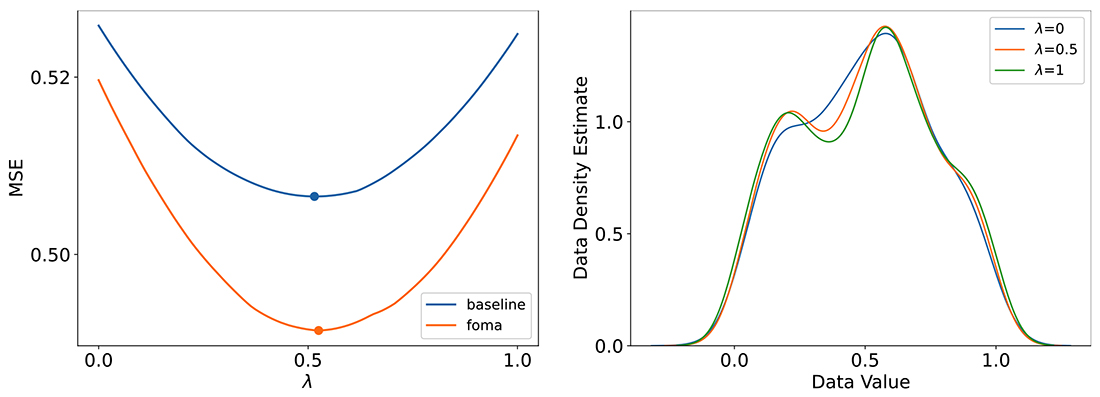
Ilya Kaufman and Omri Azencot. ICML, 2024. Abstract Data augmentation (DA) methods tailored to specific domains generate synthetic samples by applying transformations that are appropriate for the characteristics of the underlying data domain, such as rotations on images and time warping on time series data. In contrast, domain-independent approaches, e.g. mixup, are applicable to various data modalities, and as such they are general and versatile. While regularizing classification tasks via DA is a well-explored research topic, the effect of DA on regression problems received less attention. To bridge this gap, we study the problem of domain-independent augmentation for regression, and…
Sequential Disentanglement by Extracting Static Information From A Single Sequence Element
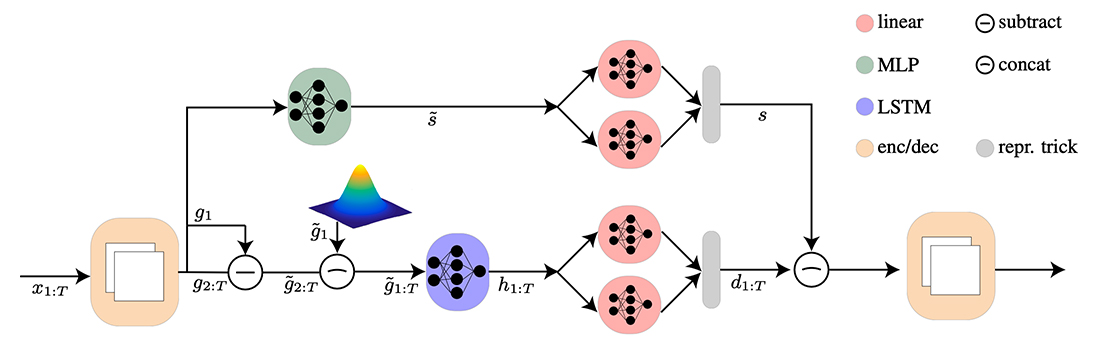
Nimrod Berman*, Ilan Naiman*, Idan Arbiv*, Gal Fadlon* and Omri Azencot. * joint first authors ICML, 2024. Abstract One of the fundamental representation learning tasks is unsupervised sequential disentanglement, where latent codes of inputs are decomposed to a single static factor and a sequence of dynamic factors. To extract this latent information, existing methods condition the static and dynamic codes on the entire input sequence. Unfortunately, these models often suffer from information leakage, i.e., the dynamic vectors encode both static and dynamic information, or vice versa, leading to a non-disentangled representation. Attempts to alleviate this problem via reducing the dynamic…
Sample and Predict Your Latent: Modality-free Sequential Disentanglement via Contrastive Estimation
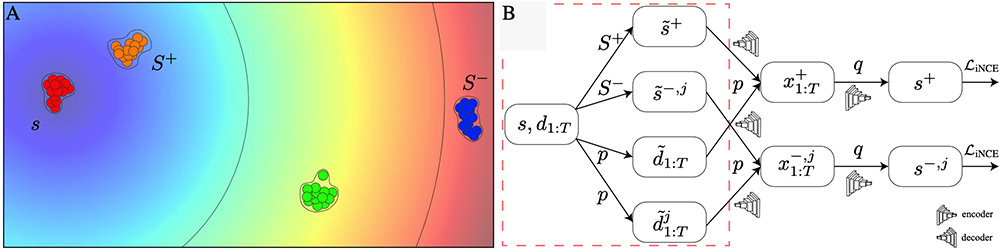
Ilan Naiman*, Nimrod Berman*, and Omri Azencot. * joint first authors ICML, 2023. Abstract Unsupervised disentanglement is a long-standing challenge in representation learning. Recently, self-supervised techniques achieved impressive results in the sequential setting, where data is time-dependent. However, the latter methods employ modality-based data augmentations and random sampling or solve auxiliary tasks. In this work, we propose to avoid that by generating, sampling, and comparing empirical distributions from the underlying variational model. Unlike existing work, we introduce a self-supervised sequential disentanglement framework based on contrastive estimation with \emph{no} external signals, while using common batch sizes and samples from the latent…
Data Representations’ Study of Latent Image Manifolds
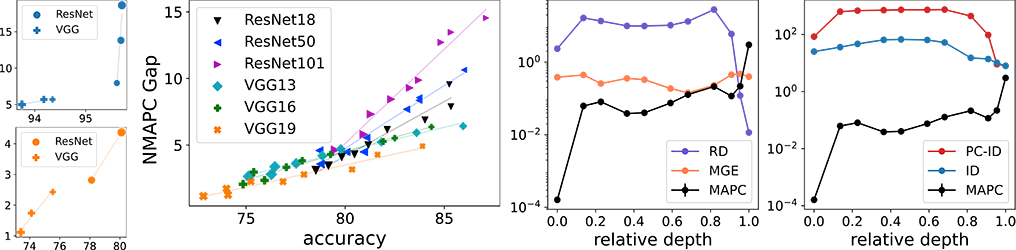
Ilya Kaufman, and Omri Azencot. ICML, 2023. Abstract Deep neural networks have been demonstrated to achieve phenomenal success in many domains, and yet their inner mechanisms are not well understood. In this paper, we investigate the curvature of image manifolds, i.e., the manifold deviation from being flat in its principal directions. We find that state-of-the-art trained convolutional neural networks for image classification have a characteristic curvature profile along layers: an initial steep increase, followed by a long phase of a plateau, and followed by another increase. In contrast, this behavior does not appear in untrained networks in which the curvature…
Forecasting Sequential Data Using Consistent Koopman Autoencoders
Omri Azencot, Benjamin Erichson, Vanessa Lin, and Michael Mahoney. International Conference on Machine Learning (ICML), 2020. Abstract Recurrent neural networks are widely used on time series data, yet such models often ignore the underlying physical structures in such sequences. A new class of physics-based methods related to Koopman theory has been introduced, offering an alternative for processing nonlinear dynamical systems. In this work, we propose a novel Consistent Koopman Autoencoder model which, unlike the majority of existing work, leverages the forward and backward dynamics. Key to our approach is a new analysis which explores the interplay between consistent dynamics and…