Generative Modeling of Regular and Irregular Time Series Data via Koopman VAEs
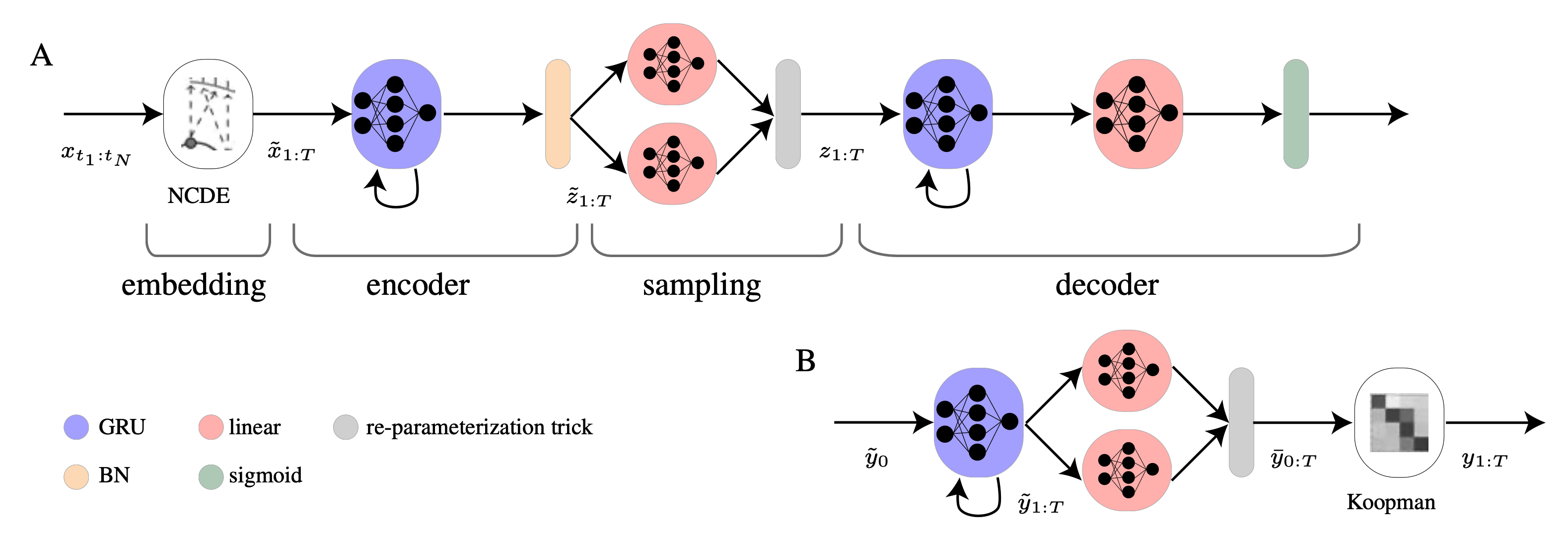
Ilan Naiman, N. Benjamin Erichson, Pu Ren, Michael Mahoney, and Omri Azencot. ICLR, 2024. Abstract Generating realistic time series data is important for many engineering and scientific applications. Existing work tackles this problem using generative adversarial networks (GANs). However, GANs are often unstable during training, and they can suffer from mode collapse. While variational autoencoders (VAEs) are known to be more robust to the these issues, they are (surprisingly) less often considered for time series generation. In this work, we introduce Koopman VAE (KoVAE), a new generative framework that is based on a novel design for the model prior, and…
Multifactor Sequential Disentanglement via Structured Koopman Autoencoders
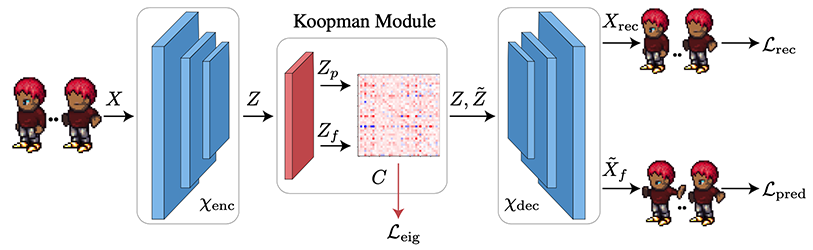
Nimrod Berman*, Ilan Naiman*, and Omri Azencot. * joint first authors ICLR, 2023. notable-top-25%! Abstract Disentangling complex data to its latent factors of variation is a fundamental task in representation learning. Existing work on sequential disentanglement mostly provides two factor representations, i.e., it separates the data to time-varying and time-invariant factors. In contrast, we consider multifactor disentanglement in which multiple (more than two) semantic disentangled components are generated. Key to our approach is a strong inductive bias where we assume that the underlying dynamics can be represented linearly in the latent space. Under this assumption, it becomes natural to exploit…
Lipschitz Recurrent Neural Networks
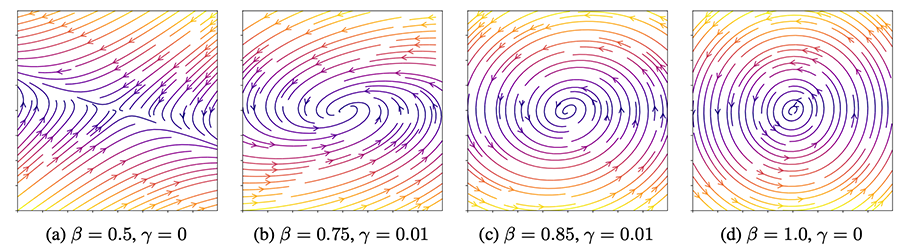
Benjamin Erichson, Omri Azencot, Alejandro Queiruga, Liam Hodgkinson, and Michael Mahoney. International Conference on Learning Representations (ICLR), 2021. Abstract Viewing recurrent neural networks (RNNs) as continuous-time dynamical systems, we propose a recurrent unit that describes the hidden state’s evolution with two parts: a well-understood linear component plus a Lipschitz nonlinearity. This particular functional form facilitates stability analysis of the long-term behavior of the recurrent unit using tools from nonlinear systems theory. In turn, this enables architectural design decisions before experimentation. Sufficient conditions for global stability of the recurrent unit are obtained, motivating a novel scheme for constructing hidden-to-hidden matrices. Our…